CIRCUITOS ELÉTRICOS III
Dado um circuito RC ( resistor e capacitor ) série, no tempo t=0 segundos, fonte de tensão de 1 V é acoplada ao circuito causando o carregamento do capacitor, determine no instante de 9 segundos. ( Sabemos : C = 5 mF, R = 2 Kohm(s), considere todos os valores iniciais iguais a zero )
- O valor da tensão no capacitor.
- O valor da tensão no resistor.
- O valor da corrente total.
V(capacitor) = 0.30 V ,V(resistor) = 0.08 V e I(total) = 8.20 mA
V(capacitor) = -4.41 V ,V(resistor) = -2.59 V e I(total) = 8.20 mA
V(capacitor) = 0.59 V ,V(resistor) = 0.41 V e I(total) = 0.20 mA
V(capacitor) = 4.59 V ,V(resistor) = 10.41 V e I(total) = 0.20 mA
V(capacitor) = 2.97 V ,V(resistor) = 0.81 V e I(total) = 2.20 mA
Um circuito RL série de primeira ordem apresenta uma tensão de entrada 1 V sendo um degrau unitário para t > 0 segundo, determine a tensão do resistor no tempo de 2 ms. Sabendo que o indutor é 7 mH e o resistor de 9 ohms e seus valores iniciais iguais a zero.
-2.07643 V
4.92357 V
1.84715 V
0.23089 V
0.92357 V
A chave do circuito abaixo esteve fechada por um longo período, sendo aberta em t=0, determine Vc(t) para t>0 sendo Vs = 3 V, R1 = 5 ohms, R2= 8 ohms e C1 = 4 mf.
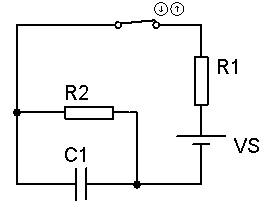
3.846 . exp( - 37.25 . t)
0.923 . exp( - 3.12 . t)
-3.154 . exp( - 23.25 . t)
1.846 . exp( - 31.25 . t)
9.231 . exp( - 187.50 . t)
Um dado capacitor (6 mF )carregado com uma tensão incial de 7 V, é acoplado a um resistor de 2 Kohms, determine o valor da tensão no capacitor quando o tempo atingir duas vezes a constante de tempo do circuito.
V(capacitor) = -3.05 V
V(capacitor) = 3.95 V
V(capacitor) = 0.95 V
V(capacitor) = 1.89 V
V(capacitor) = 0.19 V
Determine a constante de tempo aproximada, do circuito apresentado abaixo:
4000
40
0.4
4
400
O circuito série RCL apresenta C = 1 F, L= 2 H e R = 3 ohms, determine a sua frequência natural ou de ressonância wo.
1.41 radianos / segundo
0.71 radianos / segundo
0.14 radianos / segundo
-0.29 radianos / segundo
2.71 radianos / segundo
Determine a função de transferência que relaciona a tensão de entrada Vi(t) com a tensão do capacitor Vc(s) de um circuito série de 2° ordem série, sabendo que o resistor é igual a 10 Kohms, indutor = 2 mH, capacitor = 2 mF.
Vc(s)/Vi(s)=1/( 4.00 u . s² + 20.00 . s + 1)
Vc(s)/Vi(s)=1/( 6.00 u . s² + 26.00 . s + 1)
Vc(s)/Vi(s)=1/( 1.00 u . s² + 13.00 . s + 1)
Vc(s)/Vi(s)=1/( 2.00 u . s² + 2.00 . s + 1)
Vc(s)/Vi(s)=1/( 20.00 u . s² + 100.00 . s + 1)
Dada a afirmação, complete a lacuna com a alternativa que melhor represeta a porcentagem da amplitude do valor medido : "A constante de tempo 
é o tempo nescessário para o sinal atingir _________ do seu valor inicial ou final."
- O valor da tensão no capacitor.
- O valor da tensão no resistor.
- O valor da corrente total.
V(capacitor) = 0.30 V ,V(resistor) = 0.08 V e I(total) = 8.20 mA
V(capacitor) = -4.41 V ,V(resistor) = -2.59 V e I(total) = 8.20 mA
V(capacitor) = 0.59 V ,V(resistor) = 0.41 V e I(total) = 0.20 mA
V(capacitor) = 4.59 V ,V(resistor) = 10.41 V e I(total) = 0.20 mA
V(capacitor) = 2.97 V ,V(resistor) = 0.81 V e I(total) = 2.20 mA
Um circuito RL série de primeira ordem apresenta uma tensão de entrada 1 V sendo um degrau unitário para t > 0 segundo, determine a tensão do resistor no tempo de 2 ms. Sabendo que o indutor é 7 mH e o resistor de 9 ohms e seus valores iniciais iguais a zero.
-2.07643 V
4.92357 V
1.84715 V
0.23089 V
0.92357 V
A chave do circuito abaixo esteve fechada por um longo período, sendo aberta em t=0, determine Vc(t) para t>0 sendo Vs = 3 V, R1 = 5 ohms, R2= 8 ohms e C1 = 4 mf.
3.846 . exp( - 37.25 . t)
0.923 . exp( - 3.12 . t)
-3.154 . exp( - 23.25 . t)
1.846 . exp( - 31.25 . t)
9.231 . exp( - 187.50 . t)
Um dado capacitor (6 mF )carregado com uma tensão incial de 7 V, é acoplado a um resistor de 2 Kohms, determine o valor da tensão no capacitor quando o tempo atingir duas vezes a constante de tempo do circuito.
V(capacitor) = -3.05 V
V(capacitor) = 3.95 V
V(capacitor) = 0.95 V
V(capacitor) = 1.89 V
V(capacitor) = 0.19 V
Determine a constante de tempo aproximada, do circuito apresentado abaixo:
4000
40
0.4
4
400
O circuito série RCL apresenta C = 1 F, L= 2 H e R = 3 ohms, determine a sua frequência natural ou de ressonância wo.
1.41 radianos / segundo
0.71 radianos / segundo
0.14 radianos / segundo
-0.29 radianos / segundo
2.71 radianos / segundo
Determine a função de transferência que relaciona a tensão de entrada Vi(t) com a tensão do capacitor Vc(s) de um circuito série de 2° ordem série, sabendo que o resistor é igual a 10 Kohms, indutor = 2 mH, capacitor = 2 mF.
Vc(s)/Vi(s)=1/( 4.00 u . s² + 20.00 . s + 1)
Vc(s)/Vi(s)=1/( 6.00 u . s² + 26.00 . s + 1)
Vc(s)/Vi(s)=1/( 1.00 u . s² + 13.00 . s + 1)
Vc(s)/Vi(s)=1/( 2.00 u . s² + 2.00 . s + 1)
Vc(s)/Vi(s)=1/( 20.00 u . s² + 100.00 . s + 1)
Dada a afirmação, complete a lacuna com a alternativa que melhor represeta a porcentagem da amplitude do valor medido : "A constante de tempo é o tempo nescessário para o sinal atingir _________ do seu valor inicial ou final."
-2.07643 V
4.92357 V
1.84715 V
0.23089 V
0.92357 V
A chave do circuito abaixo esteve fechada por um longo período, sendo aberta em t=0, determine Vc(t) para t>0 sendo Vs = 3 V, R1 = 5 ohms, R2= 8 ohms e C1 = 4 mf.
3.846 . exp( - 37.25 . t)
0.923 . exp( - 3.12 . t)
-3.154 . exp( - 23.25 . t)
1.846 . exp( - 31.25 . t)
9.231 . exp( - 187.50 . t)
Um dado capacitor (6 mF )carregado com uma tensão incial de 7 V, é acoplado a um resistor de 2 Kohms, determine o valor da tensão no capacitor quando o tempo atingir duas vezes a constante de tempo do circuito.
V(capacitor) = -3.05 V
V(capacitor) = 3.95 V
V(capacitor) = 0.95 V
V(capacitor) = 1.89 V
V(capacitor) = 0.19 V
Determine a constante de tempo aproximada, do circuito apresentado abaixo:
4000
40
0.4
4
400
O circuito série RCL apresenta C = 1 F, L= 2 H e R = 3 ohms, determine a sua frequência natural ou de ressonância wo.
1.41 radianos / segundo
0.71 radianos / segundo
0.14 radianos / segundo
-0.29 radianos / segundo
2.71 radianos / segundo
Determine a função de transferência que relaciona a tensão de entrada Vi(t) com a tensão do capacitor Vc(s) de um circuito série de 2° ordem série, sabendo que o resistor é igual a 10 Kohms, indutor = 2 mH, capacitor = 2 mF.
Vc(s)/Vi(s)=1/( 4.00 u . s² + 20.00 . s + 1)
Vc(s)/Vi(s)=1/( 6.00 u . s² + 26.00 . s + 1)
Vc(s)/Vi(s)=1/( 1.00 u . s² + 13.00 . s + 1)
Vc(s)/Vi(s)=1/( 2.00 u . s² + 2.00 . s + 1)
Vc(s)/Vi(s)=1/( 20.00 u . s² + 100.00 . s + 1)
Dada a afirmação, complete a lacuna com a alternativa que melhor represeta a porcentagem da amplitude do valor medido : "A constante de tempo é o tempo nescessário para o sinal atingir _________ do seu valor inicial ou final."
3.846 . exp( - 37.25 . t)
0.923 . exp( - 3.12 . t)
-3.154 . exp( - 23.25 . t)
1.846 . exp( - 31.25 . t)
9.231 . exp( - 187.50 . t)
Um dado capacitor (6 mF )carregado com uma tensão incial de 7 V, é acoplado a um resistor de 2 Kohms, determine o valor da tensão no capacitor quando o tempo atingir duas vezes a constante de tempo do circuito.
V(capacitor) = -3.05 V
V(capacitor) = 3.95 V
V(capacitor) = 0.95 V
V(capacitor) = 1.89 V
V(capacitor) = 0.19 V
Determine a constante de tempo aproximada, do circuito apresentado abaixo:
4000
40
0.4
4
400
O circuito série RCL apresenta C = 1 F, L= 2 H e R = 3 ohms, determine a sua frequência natural ou de ressonância wo.
1.41 radianos / segundo
0.71 radianos / segundo
0.14 radianos / segundo
-0.29 radianos / segundo
2.71 radianos / segundo
Determine a função de transferência que relaciona a tensão de entrada Vi(t) com a tensão do capacitor Vc(s) de um circuito série de 2° ordem série, sabendo que o resistor é igual a 10 Kohms, indutor = 2 mH, capacitor = 2 mF.
Vc(s)/Vi(s)=1/( 4.00 u . s² + 20.00 . s + 1)
Vc(s)/Vi(s)=1/( 6.00 u . s² + 26.00 . s + 1)
Vc(s)/Vi(s)=1/( 1.00 u . s² + 13.00 . s + 1)
Vc(s)/Vi(s)=1/( 2.00 u . s² + 2.00 . s + 1)
Vc(s)/Vi(s)=1/( 20.00 u . s² + 100.00 . s + 1)
Dada a afirmação, complete a lacuna com a alternativa que melhor represeta a porcentagem da amplitude do valor medido : "A constante de tempo é o tempo nescessário para o sinal atingir _________ do seu valor inicial ou final."
V(capacitor) = -3.05 V
V(capacitor) = 3.95 V
V(capacitor) = 0.95 V
V(capacitor) = 1.89 V
V(capacitor) = 0.19 V
Determine a constante de tempo aproximada, do circuito apresentado abaixo:
4000
40
0.4
4
400
O circuito série RCL apresenta C = 1 F, L= 2 H e R = 3 ohms, determine a sua frequência natural ou de ressonância wo.
1.41 radianos / segundo
0.71 radianos / segundo
0.14 radianos / segundo
-0.29 radianos / segundo
2.71 radianos / segundo
Determine a função de transferência que relaciona a tensão de entrada Vi(t) com a tensão do capacitor Vc(s) de um circuito série de 2° ordem série, sabendo que o resistor é igual a 10 Kohms, indutor = 2 mH, capacitor = 2 mF.
Vc(s)/Vi(s)=1/( 4.00 u . s² + 20.00 . s + 1)
Vc(s)/Vi(s)=1/( 6.00 u . s² + 26.00 . s + 1)
Vc(s)/Vi(s)=1/( 1.00 u . s² + 13.00 . s + 1)
Vc(s)/Vi(s)=1/( 2.00 u . s² + 2.00 . s + 1)
Vc(s)/Vi(s)=1/( 20.00 u . s² + 100.00 . s + 1)
Dada a afirmação, complete a lacuna com a alternativa que melhor represeta a porcentagem da amplitude do valor medido : "A constante de tempo é o tempo nescessário para o sinal atingir _________ do seu valor inicial ou final."
4000
40
0.4
4
400
O circuito série RCL apresenta C = 1 F, L= 2 H e R = 3 ohms, determine a sua frequência natural ou de ressonância wo.
1.41 radianos / segundo
0.71 radianos / segundo
0.14 radianos / segundo
-0.29 radianos / segundo
2.71 radianos / segundo
Determine a função de transferência que relaciona a tensão de entrada Vi(t) com a tensão do capacitor Vc(s) de um circuito série de 2° ordem série, sabendo que o resistor é igual a 10 Kohms, indutor = 2 mH, capacitor = 2 mF.
Vc(s)/Vi(s)=1/( 4.00 u . s² + 20.00 . s + 1)
Vc(s)/Vi(s)=1/( 6.00 u . s² + 26.00 . s + 1)
Vc(s)/Vi(s)=1/( 1.00 u . s² + 13.00 . s + 1)
Vc(s)/Vi(s)=1/( 2.00 u . s² + 2.00 . s + 1)
Vc(s)/Vi(s)=1/( 20.00 u . s² + 100.00 . s + 1)
Dada a afirmação, complete a lacuna com a alternativa que melhor represeta a porcentagem da amplitude do valor medido : "A constante de tempo é o tempo nescessário para o sinal atingir _________ do seu valor inicial ou final."
1.41 radianos / segundo
0.71 radianos / segundo
0.14 radianos / segundo
-0.29 radianos / segundo
2.71 radianos / segundo
Determine a função de transferência que relaciona a tensão de entrada Vi(t) com a tensão do capacitor Vc(s) de um circuito série de 2° ordem série, sabendo que o resistor é igual a 10 Kohms, indutor = 2 mH, capacitor = 2 mF.
Vc(s)/Vi(s)=1/( 4.00 u . s² + 20.00 . s + 1)
Vc(s)/Vi(s)=1/( 6.00 u . s² + 26.00 . s + 1)
Vc(s)/Vi(s)=1/( 1.00 u . s² + 13.00 . s + 1)
Vc(s)/Vi(s)=1/( 2.00 u . s² + 2.00 . s + 1)
Vc(s)/Vi(s)=1/( 20.00 u . s² + 100.00 . s + 1)
Dada a afirmação, complete a lacuna com a alternativa que melhor represeta a porcentagem da amplitude do valor medido : "A constante de tempo é o tempo nescessário para o sinal atingir _________ do seu valor inicial ou final."
Vc(s)/Vi(s)=1/( 4.00 u . s² + 20.00 . s + 1)
Vc(s)/Vi(s)=1/( 6.00 u . s² + 26.00 . s + 1)
Vc(s)/Vi(s)=1/( 1.00 u . s² + 13.00 . s + 1)
Vc(s)/Vi(s)=1/( 2.00 u . s² + 2.00 . s + 1)
Vc(s)/Vi(s)=1/( 20.00 u . s² + 100.00 . s + 1)